題目出處
33. Search in Rotated Sorted Array
難度
Medium
題目分類
Array, BinarySearch
難度
medium
個人範例程式碼 - 2022/6/7 三刷
class Solution:
def search(self, nums: List[int], target: int) -> int:
start = 0
end = len(nums) - 1
while start + 1 < end:
mid = (start + end) // 2
# print(start, mid, end)
# print(nums[start], nums[mid], nums[end])
if nums[mid] == target:
return mid
if nums[start] < nums[mid]: # front: simple go up
if nums[start] <= target < nums[mid]:
end = mid
else:
start = mid
else: # back: simple go up
if nums[mid] < target <= nums[end]:
start = mid
else:
end = mid
else:
if nums[start] == target:
return start
elif nums[end] == target:
return end
else:
return -1
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
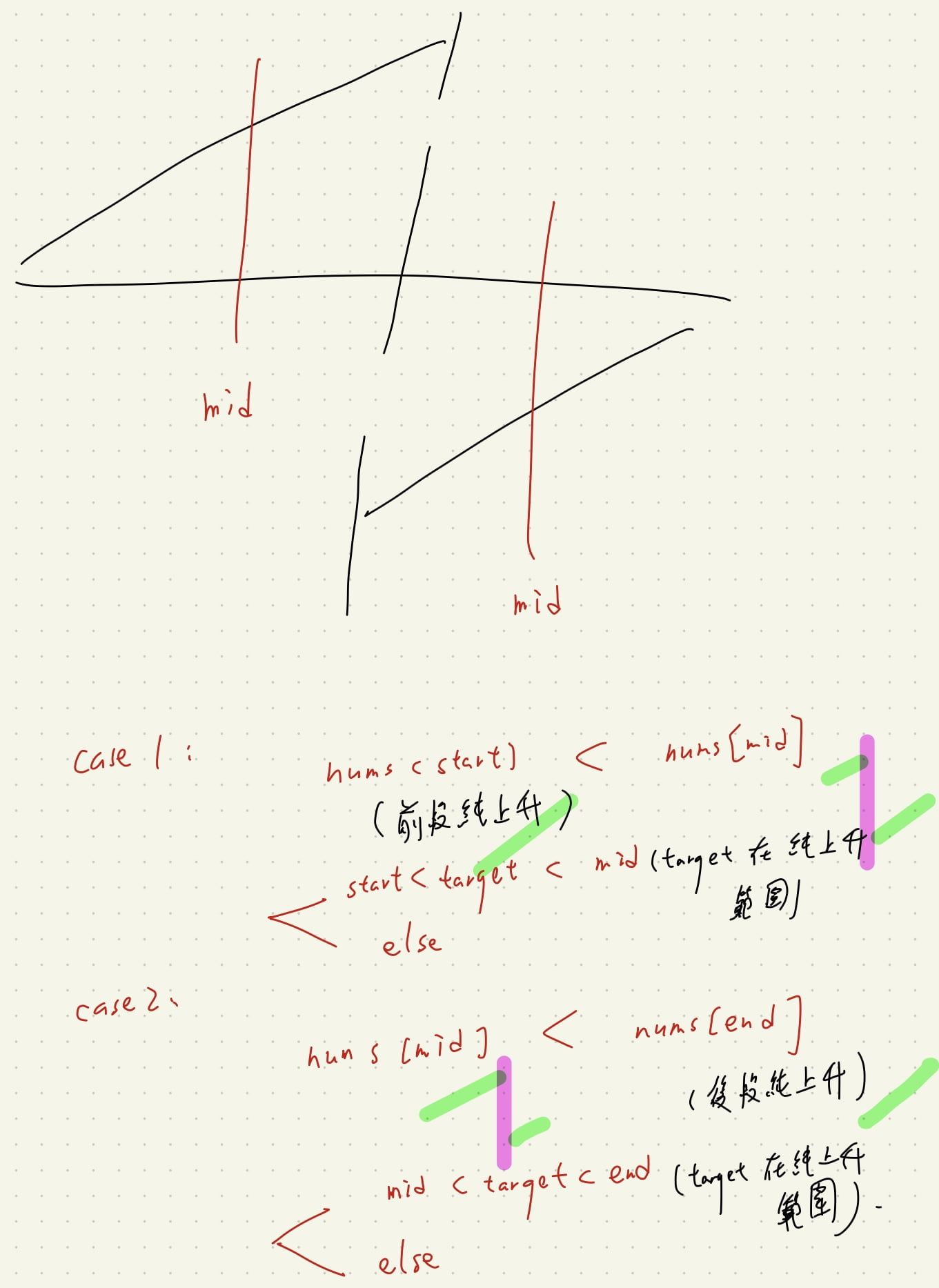
分成 2 種 case 討論,2 種 case 底下又有兩種 case,
先看 mid 的落點,
分成 「start < mid」 或 「mid < end」
再來各自看 target 的落點,(看有沒有落在單純上升的範圍)。
- 最後我們可以整理成:
- 「start < target < mid」:純上升範圍
- 「else」:亂的範圍 (依然是 rotated sorted array)
- 「mid < target < end」:純上升範圍
- 「else」:亂的範圍 (依然是 rotated sorted array)
input handling
處理沒有輸入的時候,return -1
Boundary conditions
binary search 的結束條件
個人範例程式碼 - 2022/4/5 二刷
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
start, end = 0, len(nums)-1
while(start + 1 < end):
mid = (start + end) // 2
if(nums[mid] >= nums[end]):
if(nums[start] <= target <= nums[mid]):
end = mid
else:
start = mid
else: # (nums[mid] < nums[end]):
if(nums[mid] <= target <= nums[end]):
start = mid
else:
end = mid
else:
if(nums[start] == target):
return start
elif(nums[end] == target):
return end
else:
return -1
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
這題可以說是 binary search 的最 #重要問題,
主要因為要寫得出這題,基本上要對 binary search 的各種細節幾乎都已經非常清楚才寫得出來。
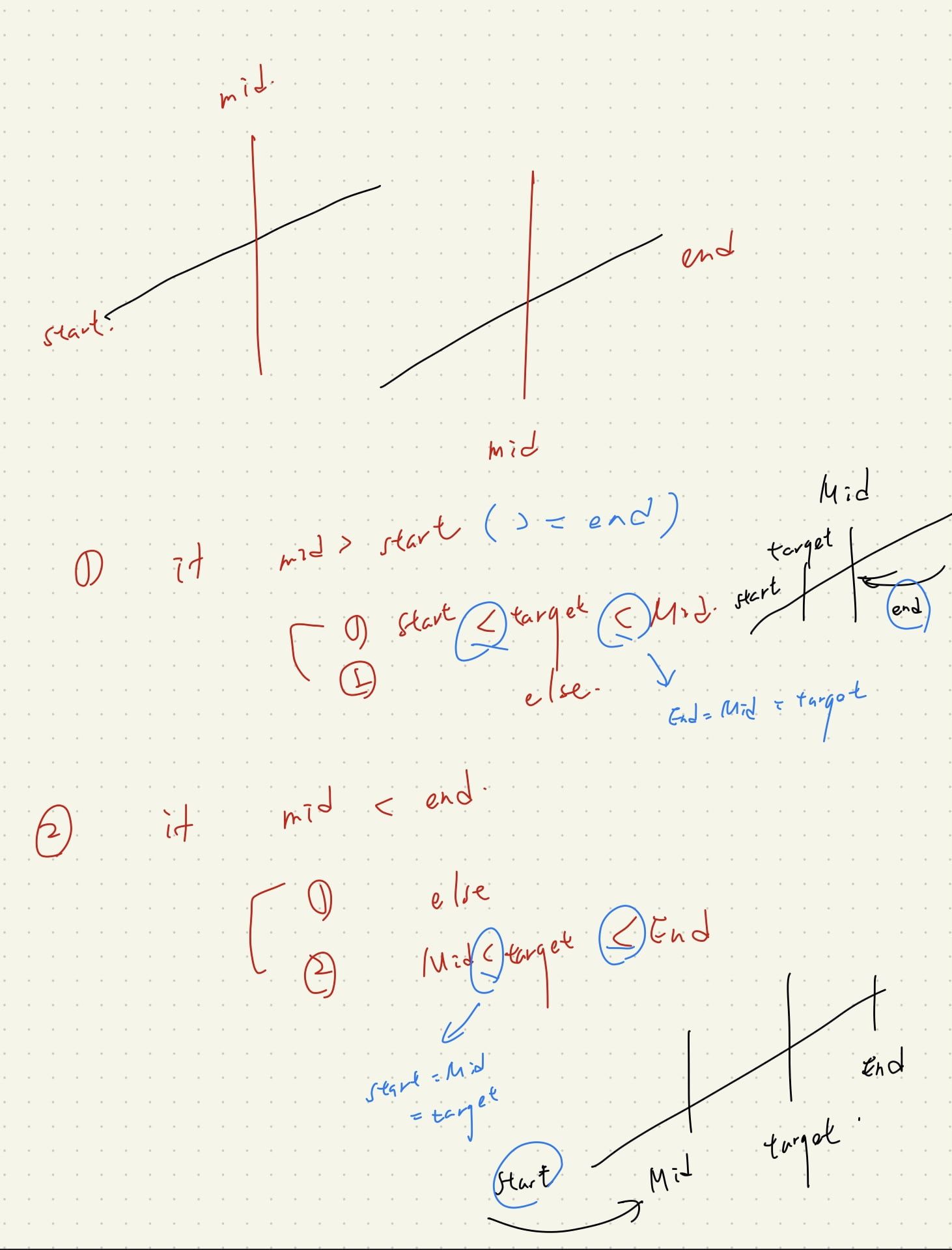
注意幾個討論的重點,我們可以把整個題目拆成 2*2 個 case,
- 比 start 還大的情況 (等同於 >= end 的情況)
- 比 end 還小的情況
然後再針對這兩個情況,再拆成兩種 mid 的情況:
- start < target < mid 的情況
- else
- else
- mid < target < end 的情況
我們要注意移動的時候要移動 start 還是 end,可以從圖上觀察而出。
此外,邊界條件的處理也是此題相當重要的關鍵。
「>= end」
這個觀念我們在 【Leetcode】python – [153] Find Minimum in Rotated Sorted Array 個人解法筆記
已經有詳細討論過,如果不清楚可以去看看
「邊界有沒有等於」?
這問題也非常重要,因為這會影響我們要移動 start 或是 end,
而我們需要讓邊界「等於」,因為如果 mid 正好是解答,
我們需要讓「移動側 = mid = target」,因此邊界條件中會有「包含等於的條件」
input handling
處理沒有輸入的時候,return -1
Boundary conditions
binary search 的結束條件
個人解法筆記 (解法重點) - 2021/7/7 一刷
示意圖
注意事項
注意 corner case 的處理
範例: [5, 1, 3]
需要注意判斷非 ascending 時,是否該值會出現在對應的區間。
個人範例程式碼
class Solution:
def search(self, nums: List[int], target: int) -> int:
l_idx , r_idx = 0, len(nums)-1
while l_idx <= r_idx:
mid_idx = (l_idx + r_idx)//2
if nums[mid_idx] == target:
return mid_idx
# search left
if nums[l_idx] <= nums[mid_idx]:
if nums[l_idx] <= target and target < nums[mid_idx]: # ascending side
r_idx = mid_idx - 1
else:
l_idx = mid_idx + 1
# search right
else:
if nums[mid_idx] < target and target <= nums[r_idx]: # ascending side
l_idx = mid_idx + 1
else:
r_idx = mid_idx - 1
return -1