題目出處
1091. Shortest Path in Binary Matrix
難度
Medium
個人範例程式碼
DIRECTIONS = [(1,1), (1,0), (0,1), (-1,1), (1,-1), (-1,0), (0,-1), (-1,-1)]
class Solution:
def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
self.m = len(grid)
self.n = len(grid[0])
return self.bfs(grid)
def bfs(self, grid):
length = 0
visited = set()
layer = [(0, 0)] # first layer
while(layer):
next_layer = []
for i, j in layer:
if self.is_valid(grid, i, j, visited):
visited.add((i, j))
if i <mark> self.m - 1 and j </mark> self.n - 1:
return length+1
for dx, dy in DIRECTIONS: # prepare for next layer
next_layer.append((i+dx, j+dy))
else:
continue
length += 1
layer = next_layer
else:
return -1 # not found
def is_valid(self, grid, i, j, visited):
return 0 <= i < self.m and 0 <= j < self.n and (i,j) not in visited and grid[i][j] == 0
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
最短路徑,我們用 BFS 去找,
因為要計算最短路徑的長度,我選擇用 layer 的方式分析,
此外,因為題目有指定 8 個方向,我另外把這 8 個變數獨立寫出來。
手動的最短路徑策略
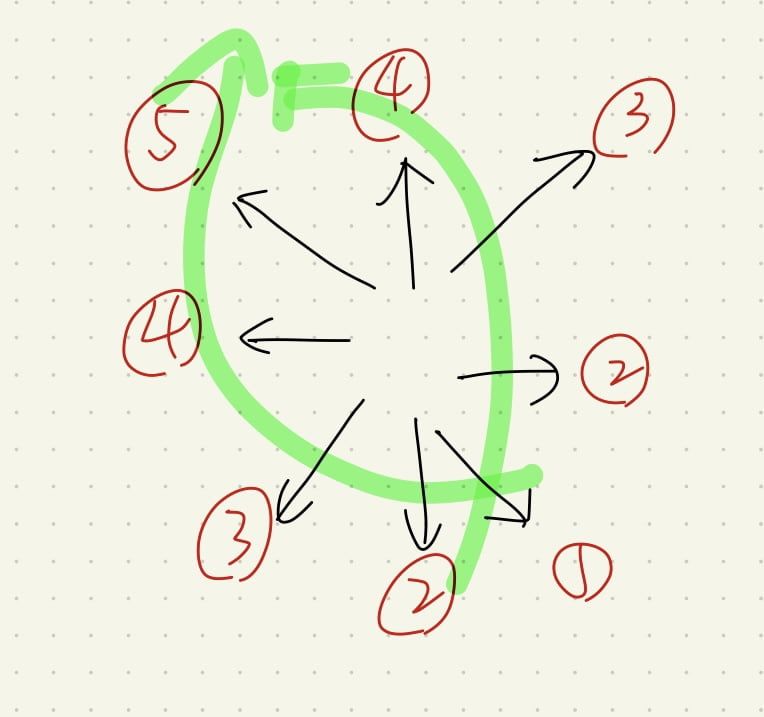
這邊注意我在設計最短路徑上是有策略的。
搜尋上,為了求最短路徑,我們當然會優先選擇「圖上往右下的部分」,
再來往下或往右,
再來往左下或右上,
以此類推,這樣我們就能優先確保先進 visited 的都是最短路徑。
- 換作程式碼如下:
DIRECTIONS = [(1,1), (1,0), (0,1), (-1,1), (1,-1), (-1,0), (0,-1), (-1,-1)]
input handling
在 bfs 一起處理,這邊注意我有踩到一個小雷。
當起點就是 1 時,注意你要怎麼處理才能回傳 -1
Boundary conditions
當 bfs 搜尋到結果後,直接 return 就是最短路徑。