710 - Python LeetCode

【Leetcode】python - [173] Binary Search Tree Iterator 個人解法筆記 #重要題型 (updated: 2022/4/22)

題目出處

173. Binary Search Tree Iterator

難度

medium

個人範例程式碼 - 2022/4/22 版本 (優化版)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class BSTIterator:

    def __init__(self, root: Optional[TreeNode]):
        self.stack = []
        self.to_left_bottom(root)

    def next(self) -> int:
        node = self.stack.pop()
        if node.right is not None:
            node_right = node.right
            self.to_left_bottom(node_right) 
        return node.val

    def hasNext(self) -> bool:
        return len(self.stack) > 0

    def to_left_bottom(self, root):
        while root:
            self.stack.append(root)
            root = root.left

# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

算法說明

與之前的相比，優化了 stack 的使用，不使用 top 的功能，只使用 pop 使程式碼更簡潔。

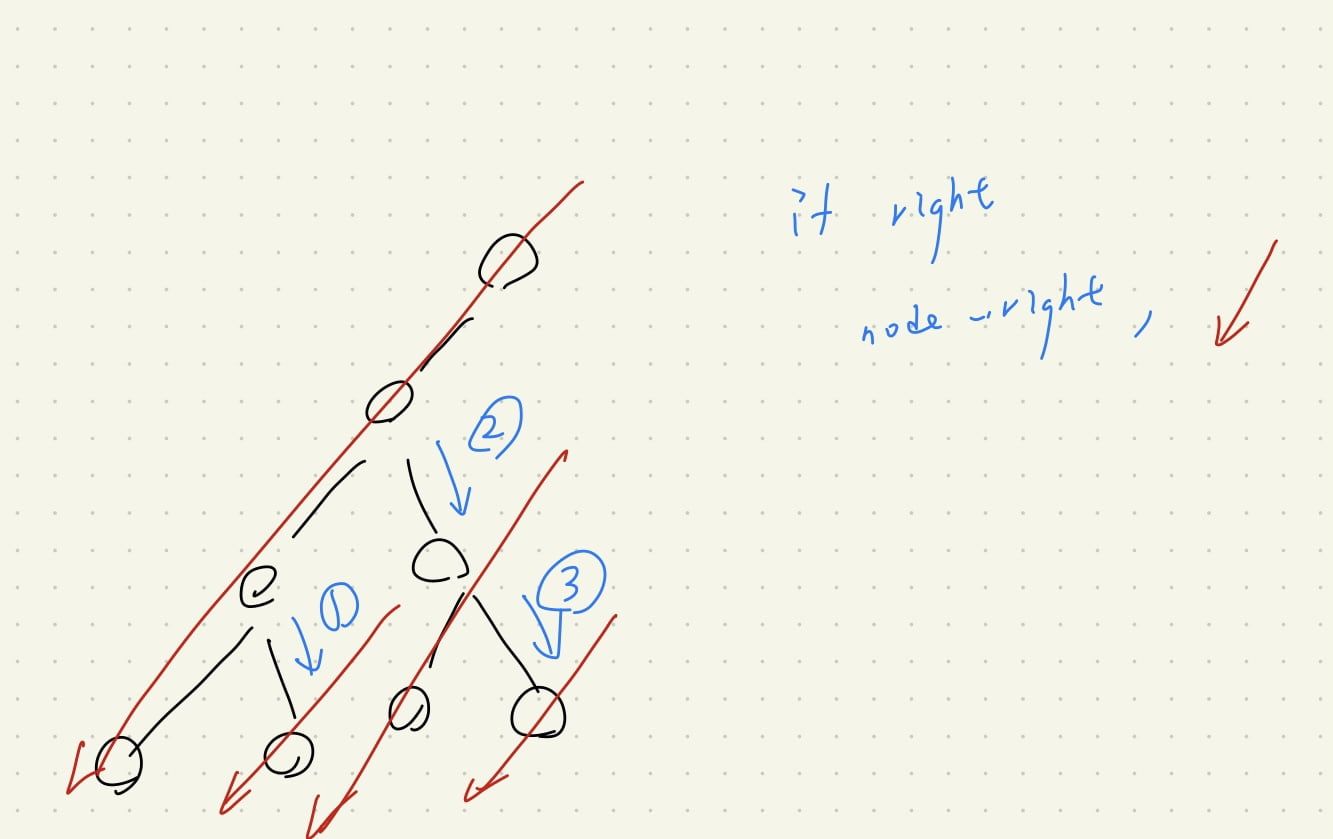
一樣保持往左走到底的觀念，不過這次我們不扣住頂端，這樣的好處是 pop 會直接回到頂端不用再用另外一個 while loop 檢查，
而只要發現能往右走，就往右走「一步」，然後依然「往左走到底」

最近在練習程式碼本身就可以自解釋的 Coding style，可以嘗試直接閱讀程式碼理解

input handling

x

Boundary conditions

當 stack 為空時，結束迴圈

個人範例程式碼 - 2022/4/21 版本

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class BSTIterator:

    def __init__(self, root: Optional[TreeNode]):
        self.stack = []
        self.to_left_bottom(root)

    def next(self) -> int:
        cur = node = self.stack[-1]
        if node.right is not None:
            node = node.right
            self.to_left_bottom(node) # do not pop parent
        else:
            node = self.stack.pop()
            while self.stack and self.stack[-1].right == node: # until parent's right = n, next node = parent
                node = self.stack.pop()

        return cur.val

    def hasNext(self) -> bool:
        return len(self.stack) > 0


    def to_left_bottom(self, root):
        while root:
            self.stack.append(root)
            root = root.left




# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

算法說明

這題考的是程式設計，很多設計上的細節需要注意。

而大方向如下：

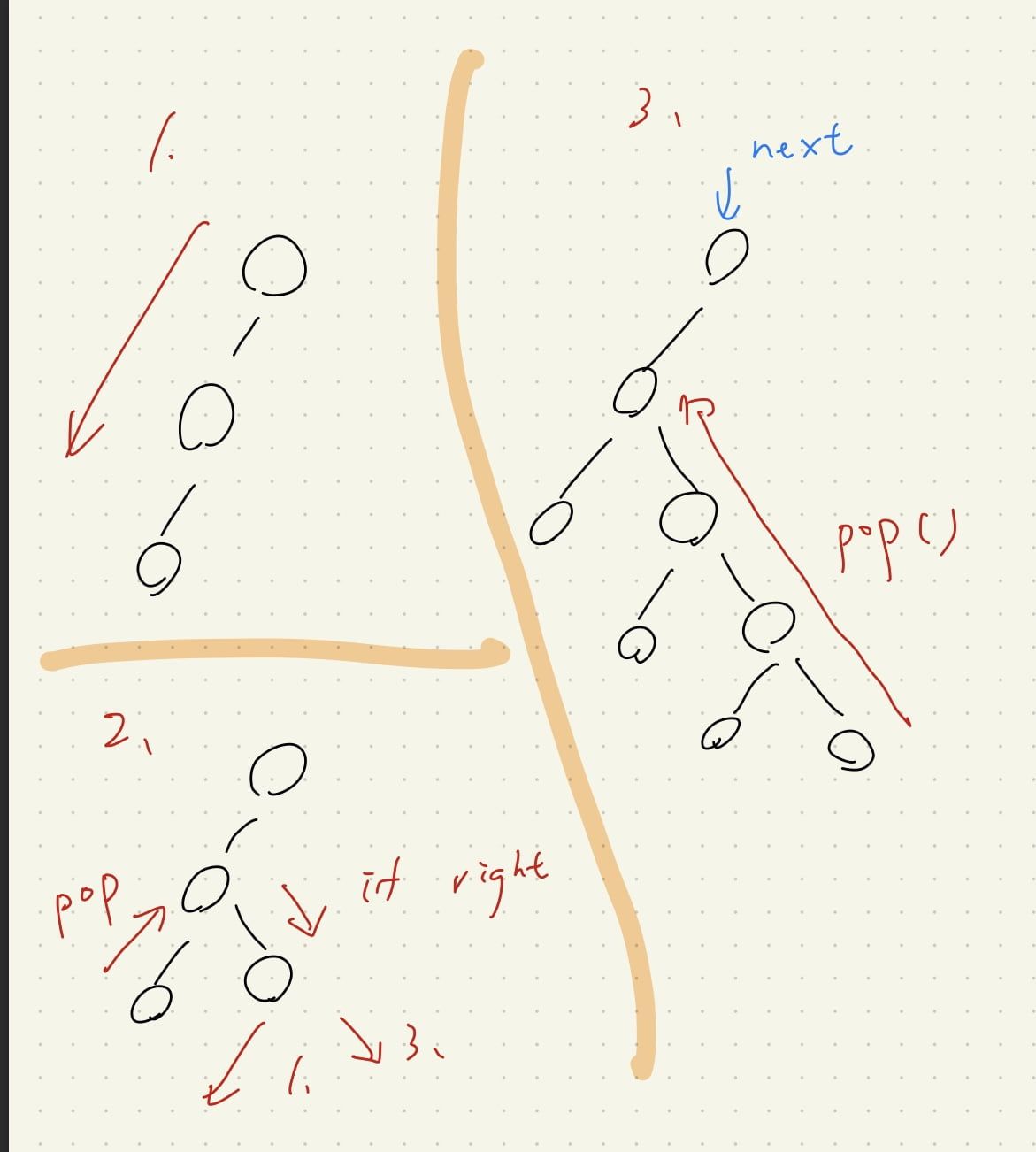
    - 當到達一個新 node 時，往左邊存 stack 直到底 - 每 pop 一個 node 時，先檢查有沒有右側，有的話一樣往右做 1 (此 node 於 stack 尚未 pop)，沒有的話做 3 - 當已經找不到右邊時，下一個節點位於「一路 pop，直到 parent.right != node」(往右走的路都退回，找第一個左彎的點)，然後他的 parent 就是我們要的下一個 node

最近在練習程式碼本身就可以自解釋的 Coding style，可以嘗試直接閱讀程式碼理解

input handling

x

Boundary conditions

當 stack 為空時，結束迴圈

Reference