710 - Python LeetCode

【Leetcode】python - [309] Best Time to Buy and Sell Stock with Cooldown 個人解法筆記

題目出處

309. Best Time to Buy and Sell Stock with Cooldown

難度

medium

個人範例程式碼

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if len(prices) <= 1:
            return 0

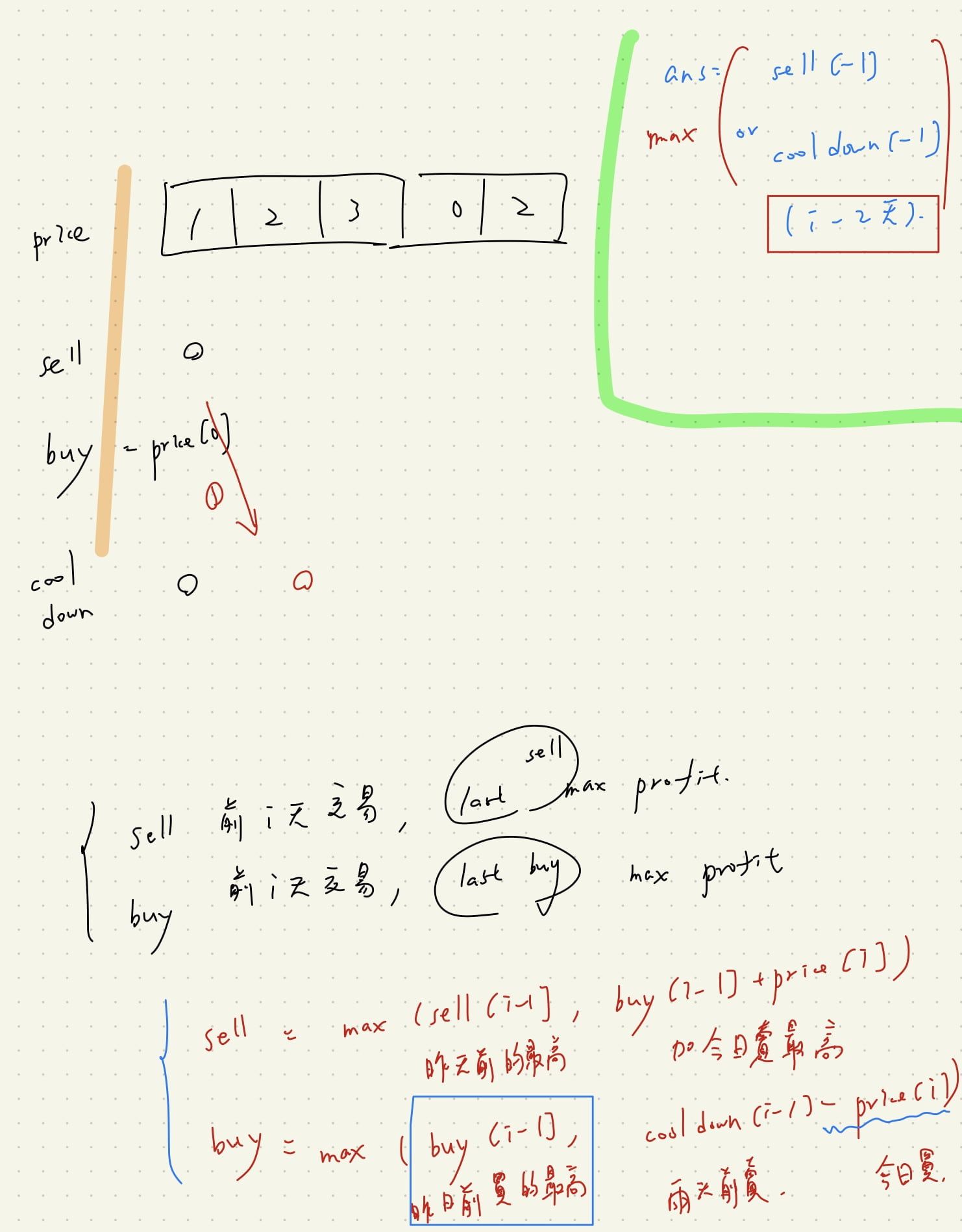
        buy = [0 for _ in range(len(prices))] # max profit, if buy today or not
        sell = [0 for _ in range(len(prices))] # max profit, if sell today or not
        cooldown = [0 for _ in range(len(prices))] # = sell[i-1]

        buy[0] = -prices[0] # init

        for i in range(1, len(prices)):
            cooldown[i] = sell[i-1]

            # if sell yesterday(or before) is max, or sell today will max
            sell[i] = max(sell[i-1], buy[i-1]+prices[i])

            # if buy yesterday(or before), or buy today will max
            # sell & cooldown both keep current max profit
            buy[i] = max(buy[i-1], cooldown[i-1]-prices[i])

        return max(cooldown[-1], sell[-1])

最近在練習程式碼本身就可以自解釋的 Coding style，可以嘗試直接閱讀程式碼理解

算法說明

要考慮滿多東西的 DP 問題，算是買賣股票系列問題中的複雜版

我們先定義主要的 DP

  • buy: 代表至當日若有任何買入，可獲得的最大 profit (可能是在 今日 或 n天前 買入)
  • sell: 代表至當日若有任何賣出，可獲得的最大 profit (可能是在 今日 或 n天前 賣出)
  • cooldown: 固定等於 sell[i-1]，是紀錄 sell 的 cooldown，供 buy 時參考

化成公式：

都有可能是今日不採取任何策略才是最好的情況，因此都會需要與昨日比較。

  • buy[i] = max(buy[i-1], cooldown[i-1]-prices[i])

cooldown[i-1]-prices[i] 代表我們拿 sell 最大 profit，並在今日買入會更大

  • sell[i] = max(sell[i-1], buy[i-1] - prices[i])

buy[i-1] - prices[i] 代表，在前 n 日買入時，在今日如果賣出，會得到更好的收益

  • cooldown[i] = sell[i-1]

這邊我們要注意的事情是，
就算 sell 在當日選擇了賣出的策略較好，
但 buy 仍會記錄最好的買入價。

因此不會因為「今日先選擇了 sell 策略」，明日「只剩下 buy 的選擇」

例子

例如: 1,2,3

分析到 2 時，也許 sell 在當日是最好的 sell[2] 策略，
但其實 sell 在 3 才是最好的，這個訊息被記錄在 buy[2] 裡面，
我們可以在 sell[3] 知道從 buy[2] 獲得最大利益。

初始化

  • buy[0] = -prices[0]
  • sell[0] = 0
  • cooldown[0] = 0

input handling

如果 len(prices) <= 1，return 0

只有小於一日，買入也是賠錢。

Boundary conditions

用 for 來控制搜尋範圍

Reference