710 - Python LeetCode

【Leetcode】python - [42] Trapping Rain Water 個人解法筆記

題目出處

42. Trapping Rain Water

難度

hard

個人範例程式碼

class Solution:
    def trap(self, height: List[int]) -> int:
        left, right = 0, len(height)-1
        max_left, max_right = height[left], height[right]
        water_contains = 0

        while(left < right):
            # print(left, right, water_contains)
            if max_left <= max_right:
                left += 1
                water_contains += self.is_positive(min(max_left, max_right) - height[left])  # current
                max_left = max(max_left, height[left])
            else:
                right -= 1
                water_contains += self.is_positive(min(max_left, max_right) - height[right]) # current
                max_right = max(max_right, height[right])

        return water_contains

    def is_positive(self, num):
        return num if num > 0 else 0

最近在練習程式碼本身就可以自解釋的 Coding style，可以嘗試直接閱讀程式碼理解

算法說明

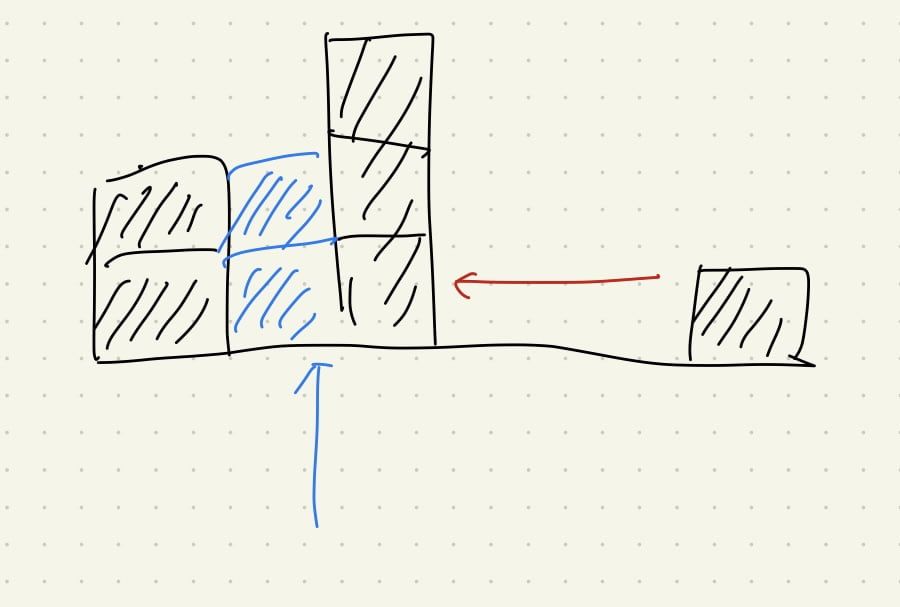
考慮比較複雜的同向 two pointer 問題。
我們需要先推導出一個公式，
「當前水位 = min(左最高, 右最高) - 當前高度」

  • 下圖的右邊，我們判斷左右高最矮的部分，可以計算當前「藍色最高為 1 」的水量 (必定，就算中間全空都會有)

  • 你可能會考慮這樣的問題，問說左邊會怎麼算到 2，如果左邊真的能算到 2， 那一定是從右邊一路過來，「有比 2 更高的事件發生 (下圖畫的不是很好，右側任意位置只要有出現比 2 更高的都可以!)」

    • 否則，左邊最高會永遠維持 1，而不用擔心算錯最主要的原因是我們不會這麼早算這格，必須確定「1 or 2」才會算 (右側有比 2 高就確定了)

    注意，處理時請注意負值

    這裡要多注意一點，處理時，
    因為我們是計算 「min(left_max, right_max) - 當前高度」，因此很有可能會有計算到負值的可能。

    這時候我們需要另外寫一個判斷式，專門處理 < 0 的情況，
    可以用我上方的方法，或是使用以下方法，
    都可以「保證最小是 0，如果 > 0 就是該值」

    max(0, min(left_max, right_max))

    input handling

    x

    Boundary conditions

    透過 while(left < right): 處理

    Reference