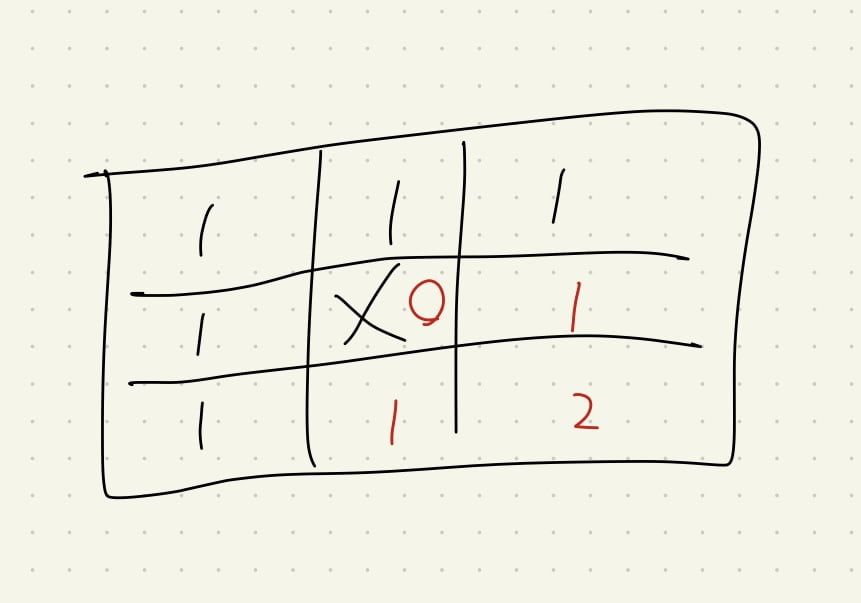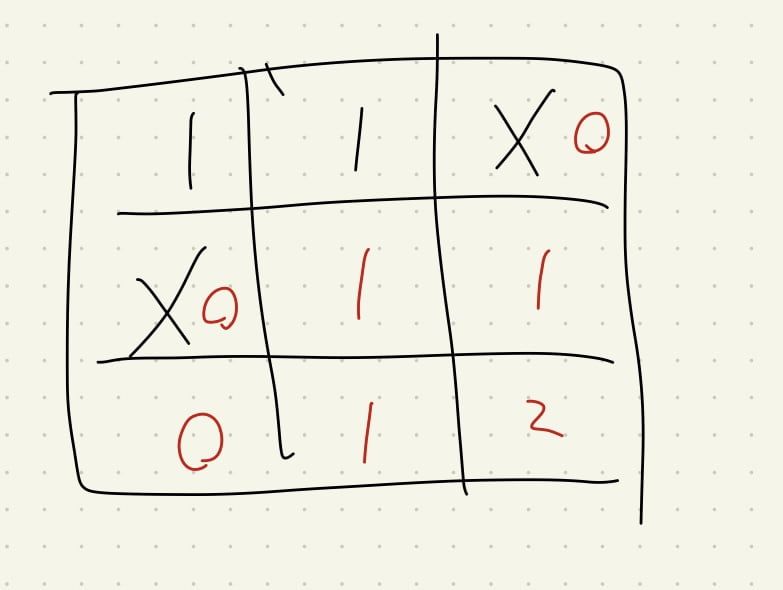題目出處
難度
Medium
個人範例程式碼
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
if not m or not n:
return 0
dp = [[0 for _ in range(n)] for _ in range(m)]
# init
if obstacleGrid[0][0] == 1:
return 0
else:
dp[0][0] = 1
for i in range(1, m):
if obstacleGrid[i][0] == 1:
dp[i][0] = 0
else:
dp[i][0] = dp[i-1][0]
for j in range(1, n):
if obstacleGrid[0][j] == 1:
dp[0][j] = 0
else:
dp[0][j] = dp[0][j-1]
# function
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
dp[i][j] = 0
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
# print(dp)
# ans
return dp[-1][-1]
算法說明
- 此題的前一題為無障礙物版本,可以參考:
https://wongwongnotes-github-io.pages.dev/python/python_leetcode/leetcode-python-62/
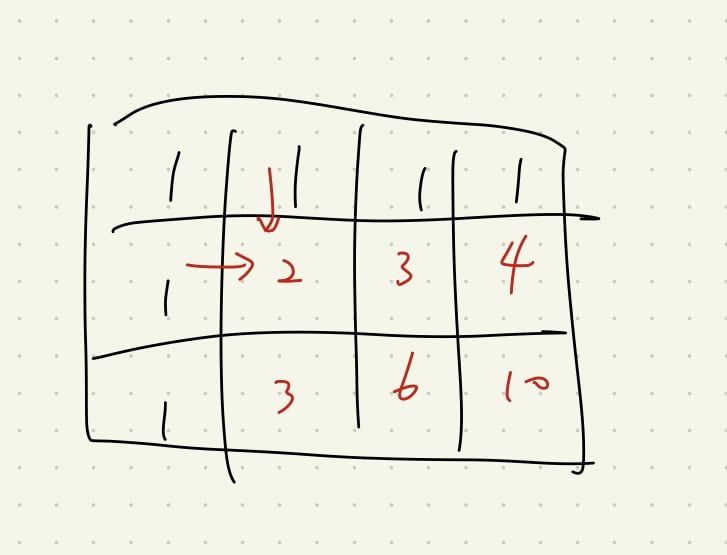
也是經典的二維 DP 問題,
透過建立下方的圖片,就可以求得所有路徑的答案
(DP 記錄到達那一格的所有方法數)
而這一題我們只需要多做處理障礙物的部分,但這次我們需要特別小心,
除了中間之外,連「邊邊初始化也要處理」
- 處理中間
- 邊邊初始化 (要多注意)
input handling
如果沒有 m 或 n,return 0 (無方法)
且如果 A[0][0] 位置就是障礙物,也是 return 0 (無方法)
Boundary conditions
用 for 來控制 DP 的範圍