題目出處
94. Binary Tree Inorder Traversal
難度
easy
題目分類
Stack, Tree, Depth-First Search, Binary Tree
解 Tree 樹問題的重點整理
這一篇的前身是以下連結,我們繼續在這篇整理重點
【Leetcode】python – [144] Binary Tree Preorder Traversal 個人解法筆記 (內含範例程式碼) 內含 處理 Tree 樹問題的重點
Tree 基本中的基本,我們一定至少需要學會兩種 parse tree 的方式,
- 一種是 iterative (直接的取)
- 另一種是 recursive (遞迴的取)
基本上這兩種都務必熟悉,未來解題時萬一一種解不出來,就可以嘗試用另外一種方法。
個人範例程式碼 - recursive 版
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
ans = []
self.dfs(root, ans)
return ans
def dfs(self, root, ans):
if root:
self.dfs(root.left, ans)
ans.append(root.val)
self.dfs(root.right, ans)
else:
return
算法說明
recursive 的 parse tree 基本上可以結合 dfs 的概念,
而我們需要另外寫一個 function dfs(),因為我們會需要把答案帶著走,原題目的函數沒辦法直接遞迴。
老實說個人覺得,Tree 系列的題目用 recursive 的概念是最接近原本學習知識觀念的解法XD。
寫起來非常直覺,而且稍微變化一下其他的解就都能直接跑出來。
主要變化的範圍如下,然後依照 (M)RL、R(M)L、RL(M) 改一下順序,全部的解法就都出來了!
- self.dfs(root.left, ans)
- ans.append(root.val)
- self.dfs(root.right, ans)
corner case 特殊情況處理
當樹為空 [] 或 為只有 root [1] 時,需要注意。
Boundary conditions/ Edge conditions 邊際情況處理
處理沒有節點的情況, if not root 直接回傳。
另外一種漂亮的解法:直接只處理 「if root:」,我們才做事情。
個人範例程式碼 - iterative 版
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
# left mid right
nodeStack = []
ans = []
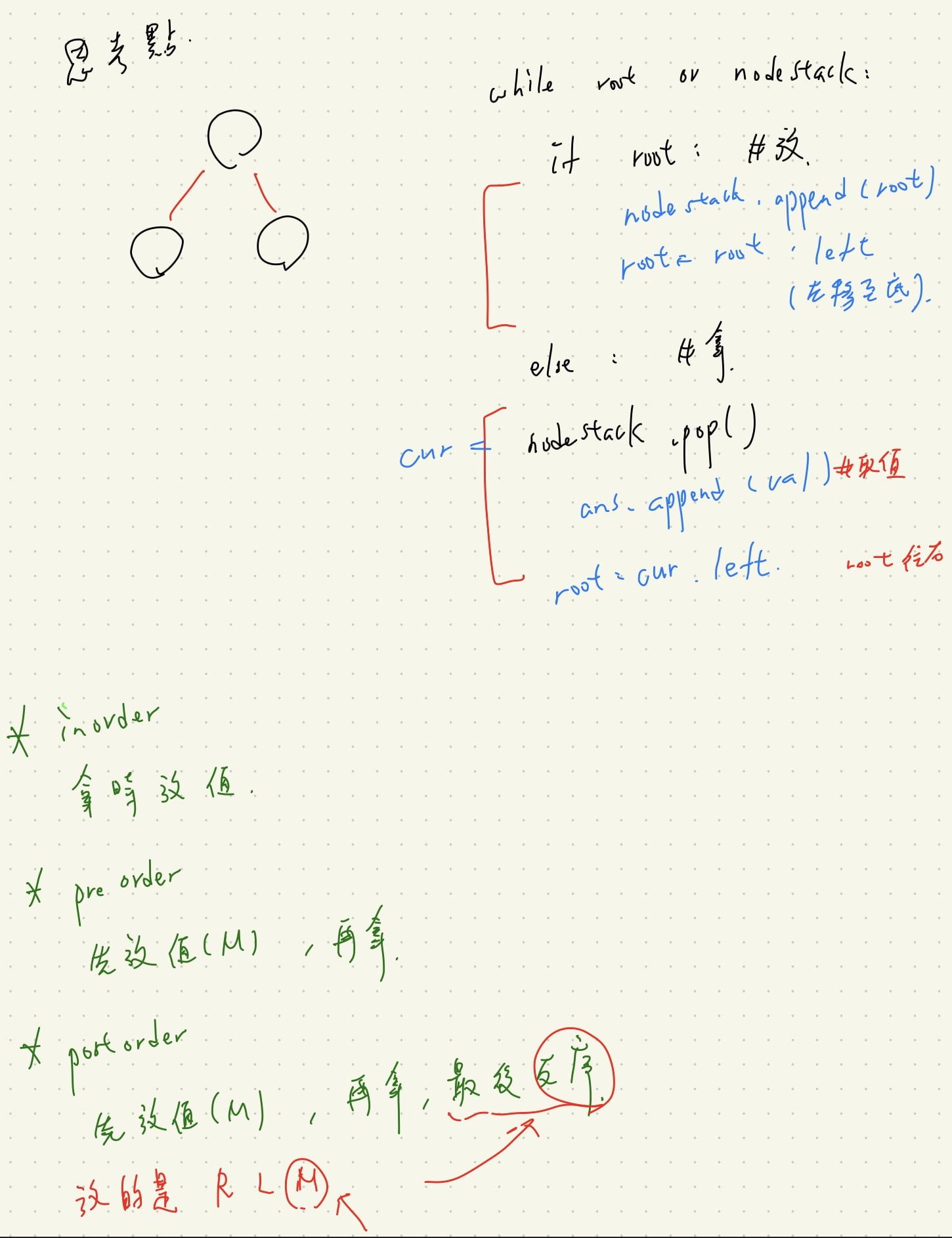
while root or nodeStack:
if root:
nodeStack.append(root)
root = root.left # repeat put left if exist
else: # nothing left
curNode = nodeStack.pop()
ans.append(curNode.val) # append left
root = curNode.right
return ans
算法說明
直覺上的解法我們需要配合 Stack,遞迴的做法我們需要配合 DFS。
Stack 為 pop() 或 pop(-1) 就可以直接實現。
- 以下筆記手寫,字醜傷眼注意XDD
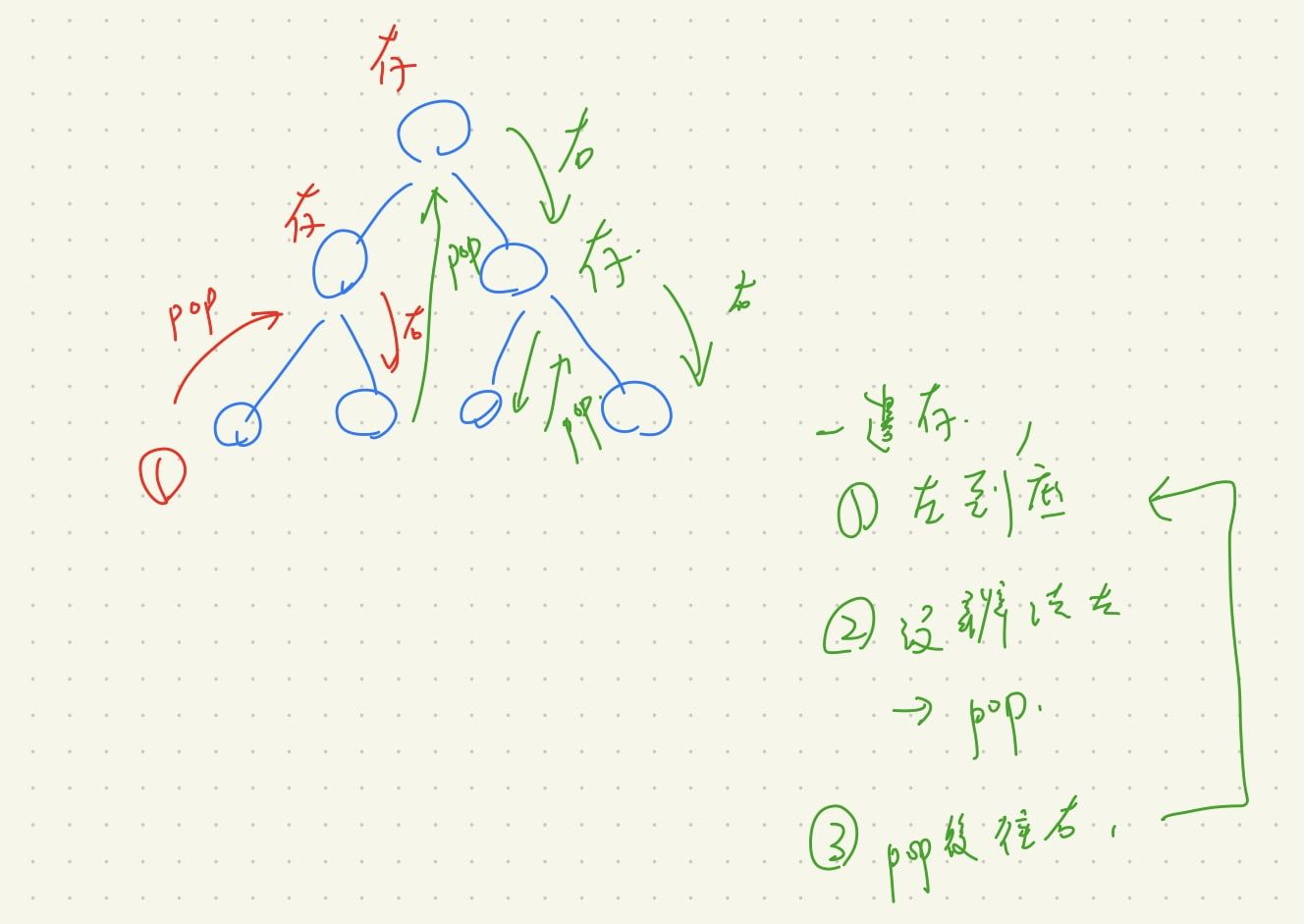
由上圖,我們可以發現,我們會先
- 向左走到底,一邊存 node 進 stack 當中,
- 發現沒辦法向左之後,pop一個值, 此值就是我們拿 inorder 中間值的時候
- pop 後往右
注意:由於「後處理要先放」,因此順序會是「先右後左」
你可能會想問這麼注意順序為什麼不用 Queue?
因為「先進先出」的結構我們沒辦法保存應該要後處理的東西。
例如 第一層的 左右,加入第二層後,
第一層的右一定會先出後,才會做第二層,因此沒辦法。
corner case 特殊情況處理
當樹為空 [] 或 為只有 root [1] 時,需要注意。
Boundary conditions/ Edge conditions 邊際情況處理
結束條件為 Stack 為空,我們運用 Stack 可以幫我們保存的概念。
結論 - 處理樹的重點
直接的解法我們需要配合 Stack,遞迴的做法我們需要配合 DFS
Stack 為 pop() 或 pop(-1) 就可以直接實現,注意「後處理要先放」。
interative 的重點
我們可以發現,不論是哪一種 interative 方法,「向左走到底都是必須的」,
因此,我們就只要專心的看何時是我們該拿值的地方,
就可以順著把這三題都解出來
我們 traversal tree 主要分成兩種情況
- 向左走到底,一邊存 node 值 (preorder 此時取值) <– (M)RL
- 無法向左的情況,從 stack pop 出一個值 (inorder 此時取值),並向右
做完第二步就繼續左到底,如果不行就 pop,如此反覆
而我們也可以分析出,類似相關的題目中
- inorder - R(M)L:拿時存答案
- preorder - (M)RL:先放值(mid),再拿
- postoreder - RL(M):先放值(mid),再拿,最後反序
postorder我們處理時會比較特別,因為他是 RL(M) 的結構,
而我們 traversal tree 時,通常都一定會先從根開始看,
因此比較好的處理方式,我們會一開始就先把順序倒過來看,
變成我們處理 (M)LR,最後再反序。