題目出處
難度
medium
個人範例程式碼
from typing import (
List,
)
class Solution:
"""
@param m: An integer m denotes the size of a backpack
@param a: Given n items with size A[i]
@return: The maximum size
"""
def back_pack(self, m: int, a: List[int]) -> int:
# write your code here
# define: dp[i][j], i = this round take, j = volume
# dp[i][j] = dp[i-1][j] # last round take
# = dp[i-1][j - A[i-1]] # inherit last take, we take new can succeed (only when j - A[i-1] >= 0)
# ans: last True dp[i][volume?]
# init: dp[all][0] = True, other False
dp = [[False]*(m+1) for _ in range(len(a)+1)] # i = m, j = count nums
dp[0][0] = True
for i in range(1, len(a)+1):
dp[i][0] = True
for j in range(1, m + 1):
dp[i][j] = dp[i-1][j]
if j - a[i-1] >= 0: # can take this
dp[i][j] = dp[i][j] or dp[i-1][j - a[i-1]]
# print(dp)
for i in range(m+1):
if dp[-1][m-i]: # check max volume
return m-i
return -1 # not found
算法說明
本題是背包系列問題的第 1 題,建議初學者可以從第一題開始去學:
第 1 題:最基本的背包問題,不重複 size,物品只有一個,計算組合可能性
第 2 題:最基本的背包問題,不重複 size,物品只有一個,計算最大價值
第 3 題:完全背包問題,有重複 size,物品無限數量,計算最大價值
第 4 題:有重複 size,物品無限數量,計算可能組合 ,「(1,2,3) 與 (2,3,1) 視為相同答案」
第 5 題:有重複 size,物品有限數量,計算可能組合 ,「(1,2,3) 與 (2,3,1) 視為相同答案」
第 6 題:有重複 size,物品無限數量,計算可能「排列」 ,也就是說「(1,2,3) 與 (2,3,1) 視為不同答案」
第 7 題:有重複物品,有限制物品數數量上限,問可能組合
第 8 題:有重複物品,有限制物品數數量上限,問最大價值
第 9 題:變化問題,有重複 size,計算機率
第 10 題:變化問題,只是把 size 面額提高
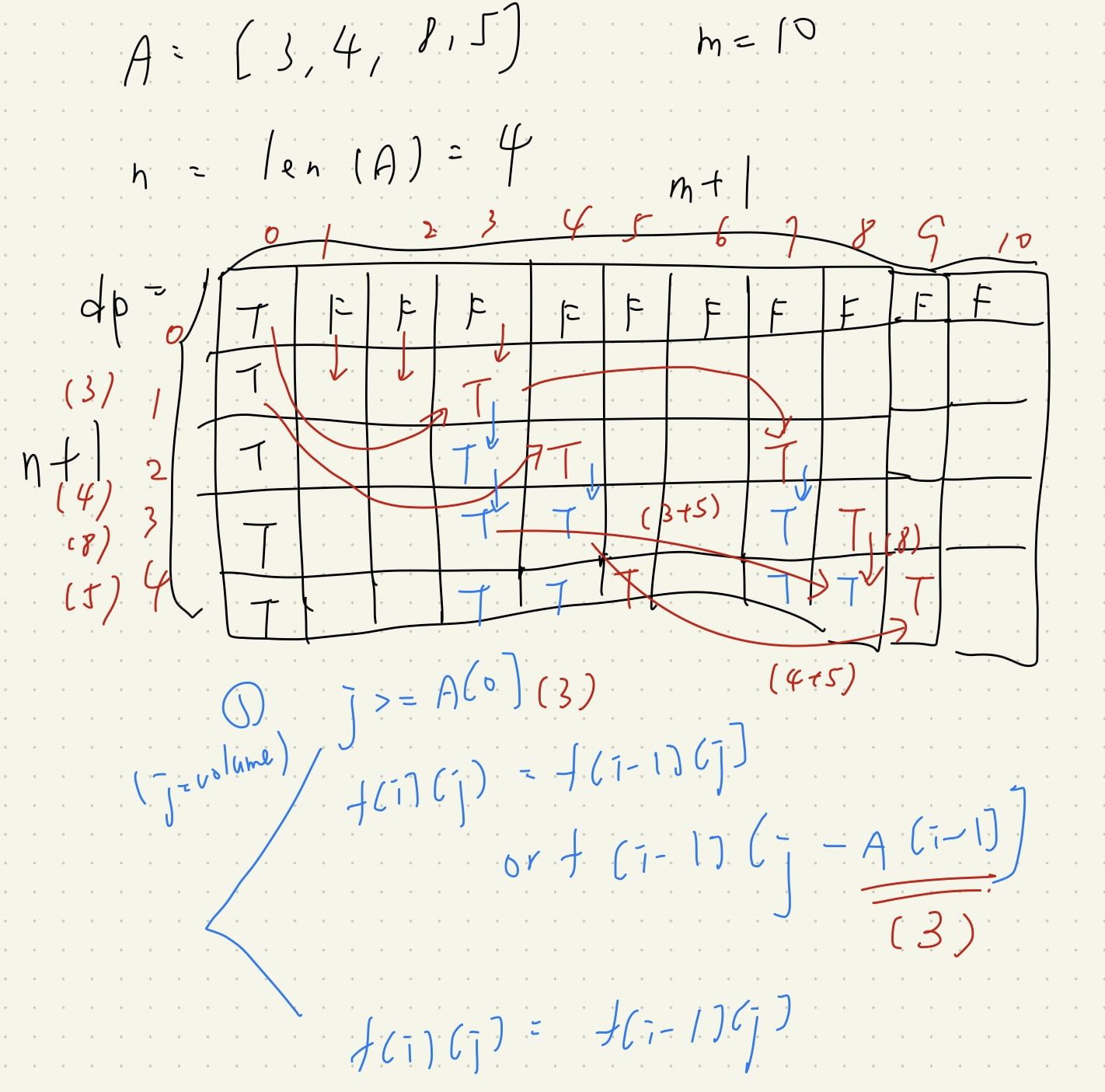
最經典的背包問題,我們用 dp 去解,
要理解背包問題,建議自己畫過一次表,會比較容易理解 DP 邏輯運作的奧妙。
用圖解析 DP 的分析過程
在這題目裡面,因為我們只有單純拿,因此我們不需要注意順序,不用花 O(nlogn) 的時間先 sort()
state
分析概念:我們建立一張表 dp[i][j], i 位置表示我們這回合要處理的新增物品,j 表示背包目前已經有的大小。
init
初始化時:dp[i][0], dp[0][j] 都為 True,其他 init 為 False
define
dp[i][j] = dp[i-1][j] # default 情況,我們複製上個階段的所有結果。
特殊情況: last_volume = j - nums[i-1] # 表示如果本次我們選擇拿新東西,是否有可能有這個組合的大小。
dp[i][j] = dp[i][j] or dp[i-1][last_volume] # 任意 True 即可
ans
dp[-1][j] # 從最大直到找到第一個 True,就是結果。
input handling
一同在 dp 內處理
Boundary conditions
用兩層 for 來控制搜尋範圍,
外層 for size (表示我們選擇新的項目)
內層 for volume (表示紀錄目前已有的選擇下,可否達到裝滿的目標)