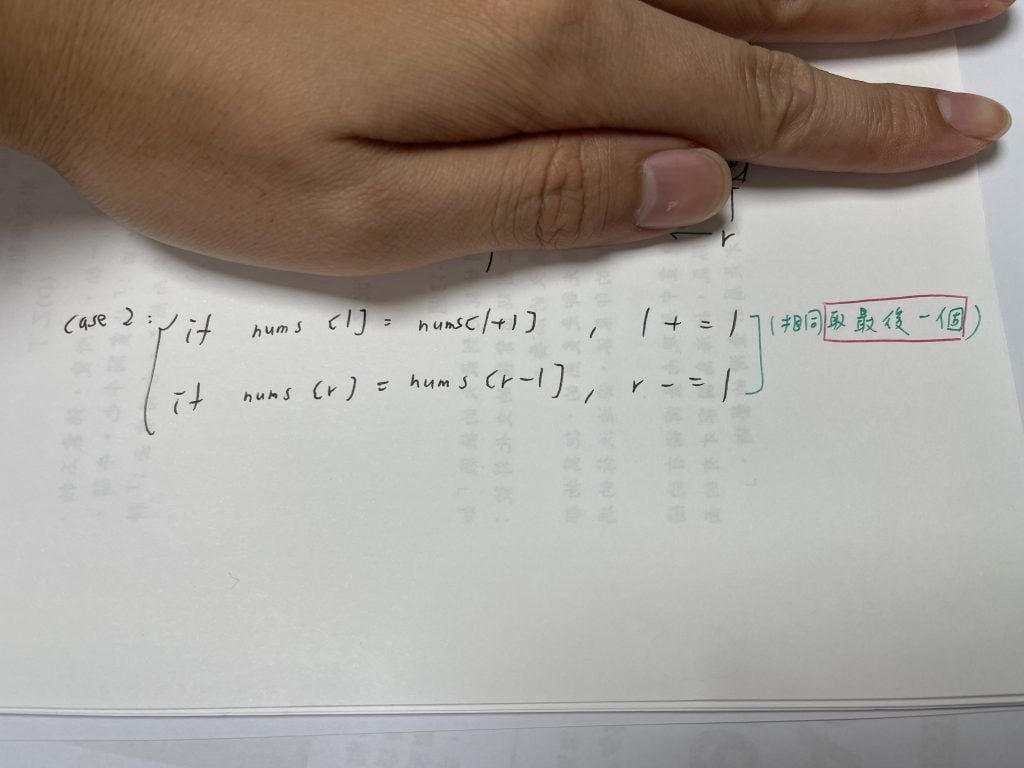題目出處
難度
Medium
題目分類
Array, TwoPointers
個人範例程式碼 - two pointers (第二次解:2022/4/6)
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
ans = []
for idx, target in enumerate(nums):
if idx > 0 and nums[idx] == nums[idx-1]: # prevent duplicate
continue
ans = self.two_sum(nums, ans, idx+1, len(nums)-1, -target)
return ans
def two_sum(self, nums, ans, start, end, target):
last_ans = []
while(start < end):
if(nums[start] + nums[end] == target):
if [-target, nums[start], nums[end]] != last_ans: # prevent duplicate
last_ans = [-target, nums[start], nums[end]]
ans.append(last_ans)
start += 1
end -= 1
elif(nums[start] + nums[end] < target):
start += 1
else: # if(nums[start] + nums[end] > target):
end -= 1
else:
return ans
算法說明
3Sum 可以當作是 2Sum 的進階版,
而變化的部分在於 target 的變化變成可以動態的,
可以視為:3Sum = 2Sum + 「動態 target」
因此我們可以沿用 2Sum 的作法,
並把 2Sum 中 target 改為動態的尋找。
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
input handling
處理 input 為 [] 的情況,應該要輸出 []。
處理 input 為 [0, 0, 0] 的情況,應該也要輸出 [[0, 0, 0]]。
Boundary conditions
有幾個重點:
防止重複 1 : 「a <= b」 <= c
防止重複的第一個部分,就是避免重複數值時,
a, b 都被重算,我們都統一取第一個去運算。
- 此外需要特別注意:因為判斷式為 「nums[idx] nums[idx-1]」,需要再多判斷一個「idx > 0」。
if idx > 0 and nums[idx] == nums[idx-1]: # prevent duplicate
continue
防止重複 2 : a <=「b <= c」
這邊基本上我們統一拿來結果來判斷,只要 b, c 組合不相同,就視為不同的解。
3. two pointers: start < end,交錯或等於就結束
two pointers 的基本結束條件。
個人解法筆記 - (第一次解:2021/4/2)
這題是第 1 題的延伸題目,這次我們要處理 3數之和 的問題。
大概念
我們將這個題目看成,「任兩數和」 等於 「負的第三數」
「負的第三數」我們稱之為我們要的 target
為了更乾淨我們處理的順序,我們會先進行「排序」
示意圖:

TwoPointers
在排序後,我們選定 target,我們使用 TwoPointers,
從左 ( l ) 開始小往大掃、從右 ( r ) 開始大往小掃,
當左( l ) 大於等於右( r ) ,也就是交錯甚至超過。
就是我們的終止條件。
示意圖:
重複處理 case1 : target 的重複
重複時的選擇:我們選擇第一個 target。
除了 target 重複會造成重複解答之外,
選擇第一個也能夠保證當解答中有與target重複的數值也能被我們考慮到。
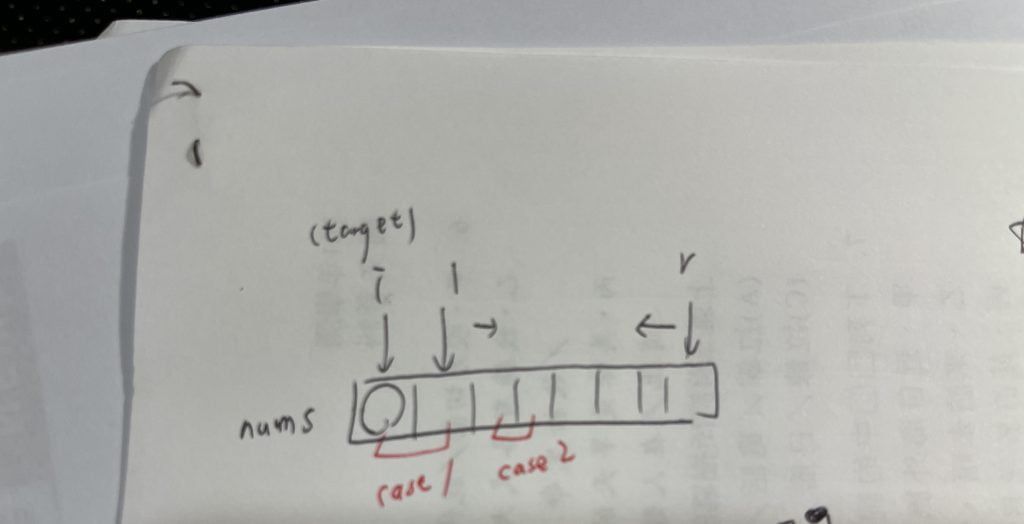
- 示意圖:(處理 target 的重複)

- 可以觀察 i 與 target 的變化,仔細思考,可以得到一些心得:

重複處理 case2 : r, l 選到值的重複
- 重複時的選擇:我們選擇「l」的第一個值,r不同時處理。
因為,當我們得到答案並更新「l」之後,對應的 nums[r] 直接不成立。
思考時,只需要思考單邊重複如何處理即可。 (多思考會錯,可以見下面錯誤區)
選擇第一個值的原因是,我們預期「剩下的值」有可能存在答案。
而當找到答案時,我們再將「l」移至下一個值 (也就是說,反覆 l+1 直到值不同)
這樣才能處理極端狀況:[0, 0, 0]
- 示意圖:(處理 l, r 的重複)

個人範例程式碼
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
ans = []
# decide target
for i in range(len(nums)):
if(i > 0 and nums[i-1] == nums[i]): # when same target, only calculate first
continue # go to next loop
target = -nums[i]
# print(f"i = {i}, target = {target}") # debug
l = i+1
r = len(nums)-1
while(l < r and l < len(nums) and r >= 0): # normal condition
# print(f"l = {l}, r = {r}") # debug
if nums[l] + nums[r] == target:
ans.append([nums[i], nums[l], nums[r]])
l += 1
while l < r and nums[l] == nums[l-1]: # when same value, only calculate first
l += 1
elif nums[l] + nums[r] > target: # need smaller, r - 1
r -= 1
else: # nums[l] + nums[r] < target: need bigger, l + 1
l += 1
return ans
「錯誤紀錄」 手繪筆記
重點:錯誤錯在兩邊同時尋找,無法解[0,0,0] 這個 case!
這題是第 1 題的延伸題目,這次我們要處理 3數之和 的問題。
大概念
我們將這個題目看成,「任兩數和」 等於 「負的第三數」
「負的第三數」我們稱之為我們要的 target
為了更乾淨我們處理的順序,我們會先進行「排序」
示意圖:

TwoPointers
在排序後,我們選定 target,我們使用 TwoPointers,
從左 ( l ) 開始小往大掃、從右 ( r ) 開始大往小掃,
當左( l ) 大於等於右( r ) ,也就是交錯甚至超過。
就是我們的終止條件。
示意圖:
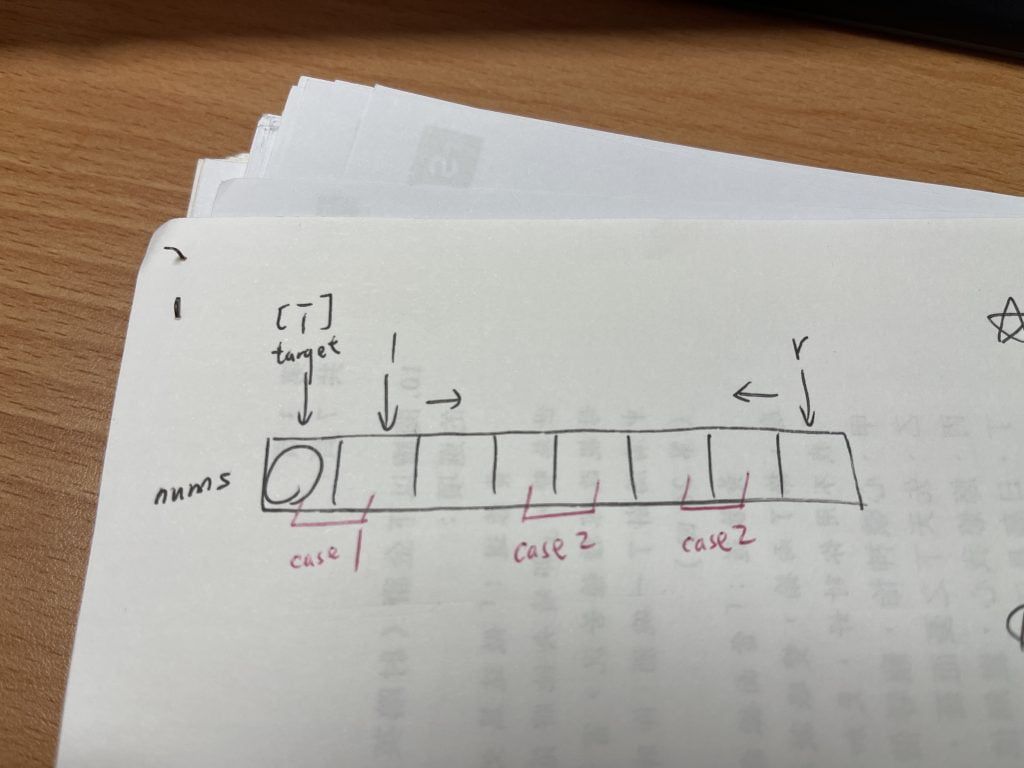
重複處理 case1 : target 的重複
重複時的選擇:我們選擇第一個 target。
除了 target 重複會造成重複解答之外,
選擇第一個也能夠保證當解答中有與target重複的數值也能被我們考慮到。
示意圖:

重複處理 case2 : r, l 選到值的重複
重複時的選擇:我們選擇最後一個值。
選擇最後一個值的原因是,我們預期「剩下兩個值」的組合應該會不同。
所以我們只看最後一個。
而且,就算真的重複了。(例如極端狀況:[0, 0, 0]) (此方法並沒有辦法處理)
我們也會先進行 -target = nums[l] + nums[r] 的檢查後,
抓出這樣的極端情況。
示意圖: