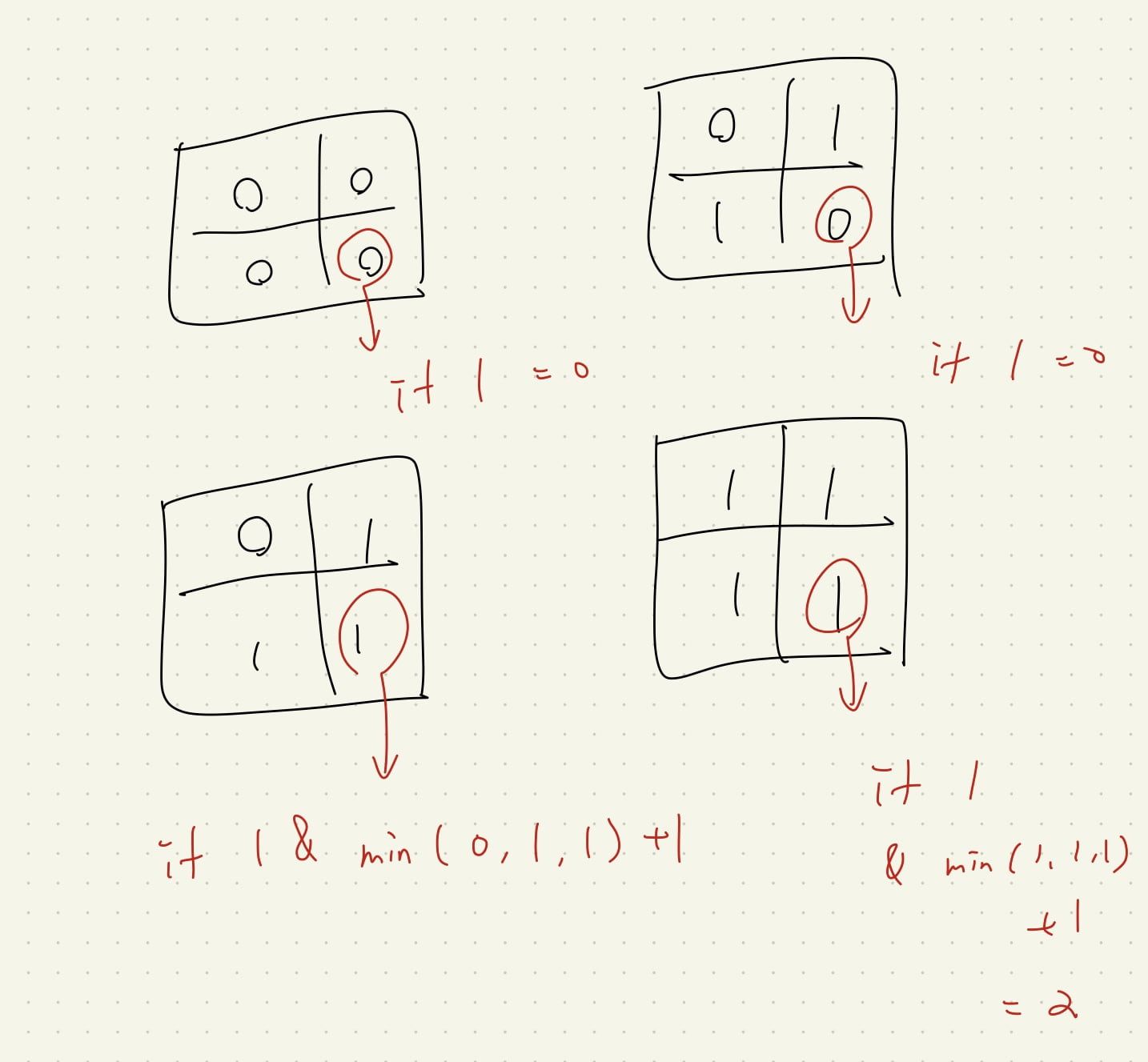題目出處
難度
medium
個人範例程式碼 - BFS (會 TLE)
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
if not matrix:
return 0
ans = 0
for i in range(len(matrix)):
for j in range(len(matrix[0])):
if matrix[i][j] == "1":
ans = max(ans, self.bfs(matrix, i, j))
return ans
def bfs(self, matrix, start_i, start_j):
edge = 1
while(True):
for i in range(start_i, start_i+edge):
for j in range(start_j, start_j+edge):
# print(i, j)
if self.is_bounded(matrix, i, j) and matrix[i][j] == "1":
continue
else:
return (edge-1)**2
edge += 1
def is_bounded(self, matrix, i, j):
m, n = len(matrix), len(matrix[0])
return 0 <= i < m and 0 <= j < n
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
BFS 應該是這題最直覺的解,不過會 TLE,需要再加速。
input handling
處理沒有 matrix 的情況,return 0
Boundary conditions
控制 for-loop 的範圍
個人範例程式碼 - DP
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
if not matrix:
return 0
dp = [list(map(int, x)) for x in matrix] # deepcopy -> int
for i in range(1, len(dp)):
for j in range(1, len(dp[0])):
dp[i][j] = self.get_max_square(dp, i, j)
# print(dp)
# print(max(max(x) for x in dp))
return max(max(x) for x in dp)**2
def get_max_square(self, dp, i, j):
if dp[i][j] == 0:
return 0
# must be 1
return min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])+1
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
概念參考自:
我們新建一個 dp,專門來記錄右下點的最大正方形「邊長」,
這個「邊長」,我們可以推出規律為:
- 如果該格是 0,就是 0 (連 1*1 正方形都不可能)
- 如果該格是 1,判斷 min([i-1][j-1], [i-1][j], [i][j-1]) + 1 ,即為此格,
意義為,如果任一格為 0,表示缺一角
如果情況為 1,2,2 也是,表示有缺一角,但仍滿足 2*2 的情況 = min(1,2,2)+1
input handling
處理沒有 matrix 的情況,return 0
Boundary conditions
控制 for-loop 的範圍