題目出處
98. Validate Binary Search Tree
難度
medium
個人範例程式碼 - DFS
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
return self.dfs(root, float("-inf"), float("inf"))
def dfs(self, root, lowerbound, upperbound):
# end of recursion
# define and split
ans = True
if root.left: # left: update upperbound
if lowerbound < root.left.val < root.val:
ans &= self.dfs(root.left, lowerbound, root.val)
else:
return False
if root.right: # right: update lowerbound
if root.val < root.right.val < upperbound:
ans &= self.dfs(root.right, root.val, upperbound)
else:
return False
return ans
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
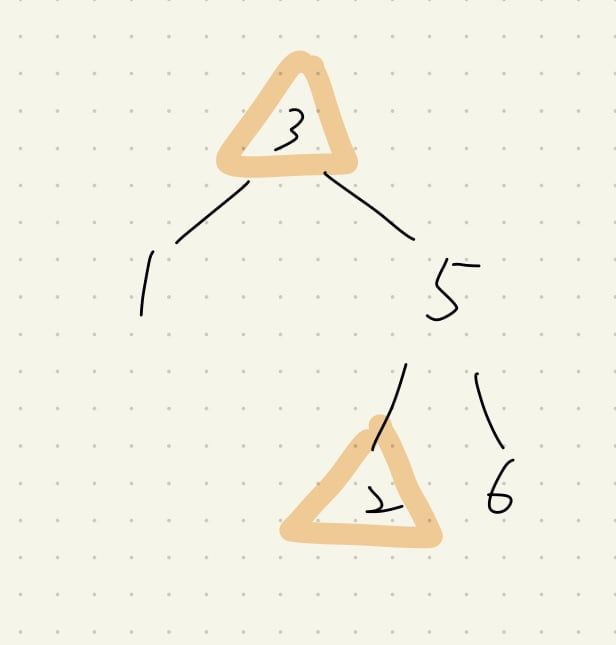
DFS 中,我們需要特別注意 BST 的特性,也就是他上下的範圍,常見錯誤如下
如果「只注意他與上層的關係」,會出現下圖中「三角形的錯誤」,因此我們需要同時考慮上下界
然而,在 BST 中處理上下界並不難,上下界的特性也十分容易分析。
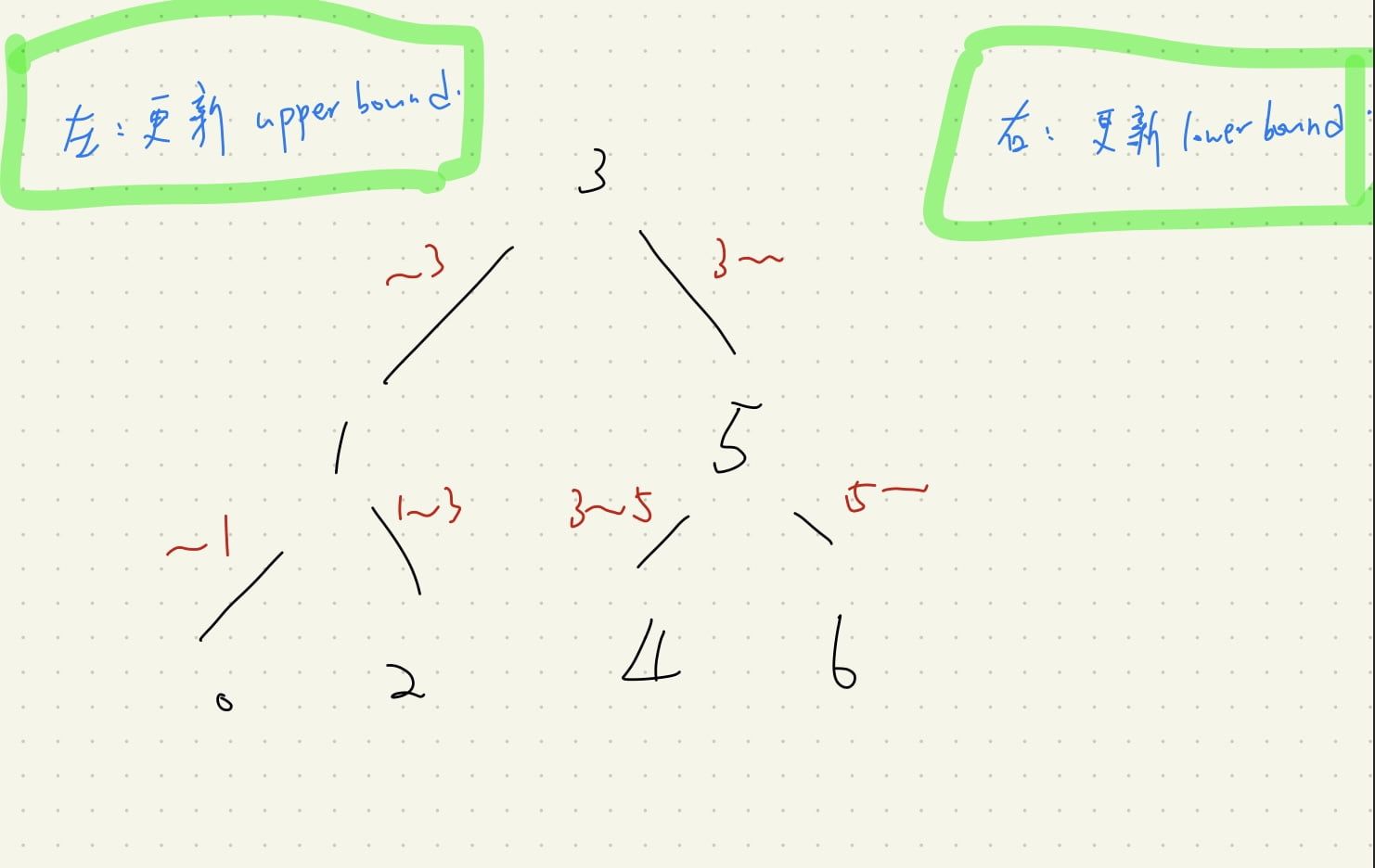
我們只需要注意兩個重點:
- 往左走時:更新 upperbound
- 往右走時:更新 lowerbound
見下圖:
input handling
同 DFS 一起處理
Boundary conditions
每個點都必須同時界於 lowerbound ~ upperbound,不然 return False
個人範例程式碼 - inorder traversal
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
stack = []
node = root
# 1. to left bottom
while node:
stack.append(node)
node = node.left
ans = []
# 2. pop right, see right, to left bottom
while stack:
node = stack.pop(-1)
ans.append(node.val)
if node.right:
node = node.right
while node: # to left bottom
stack.append(node)
node = node.left
# print(ans)
# return ans == sorted(ans)
for i, num in enumerate(ans):
if i > 0 and ans[i-1] >= ans[i]:
return False
return True
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
直接用 inorder traversal 把整個順序列出來,然後再依序比較後者必須比前者大。
input handling
如果沒有 root,return 0
Boundary conditions
inorder traversal 的 stack 流派
使用 stack
- 左到底
- pop,找右一個,然後一樣往左邊底
在 pop 時紀錄,就會得到最終答案。