題目出處
2267. Check if There Is a Valid Parentheses String Path
難度
hard
個人範例程式碼 - 純 DFS (會 TLE)
DIRECTIONS = [
(1,0),
(0,1)
]
class Solution:
def hasValidPath(self, grid: List[List[str]]) -> bool:
if not grid:
return False
return self.dfs(grid, 0, 0, set(), [])
def dfs(self, grid, i, j, visited, queue):
# print(i, j, visited, queue)
# end of recursion
if i <mark> len(grid)-1 and j </mark> len(grid[0])-1:
if grid[i][j] <mark> ")" and queue and queue[-1] </mark> "(":
return len(queue) == 1 # queue is empty
else:
return False # not ")" or queue[-1] not "("
# define and split
ans = False
visited.add((i, j))
for d_x, d_y in DIRECTIONS:
if ans == True: # Find case, early return
continue
if self.is_valid(grid, i+d_x, j+d_y) and (i+d_x, j+d_y) not in visited:
if grid[i][j] == "(":
queue.append("(")
ans |= self.dfs(grid, i+d_x, j+d_y, visited, queue)
queue.pop(-1) # backtracking
else: # ")"
if not queue:
# return False, wrong: need remove
continue
else:
queue.pop(-1) # pop ")"
ans |= self.dfs(grid, i+d_x, j+d_y, visited, queue)
queue.append(")") # backtracking
visited.remove((i, j))
return ans
def is_valid(self, grid, i, j):
m, n = len(grid), len(grid[0])
return 0 <= i < m and 0 <= j < n
算法說明
矩陣搜索,很直覺想到的就是使用 dfs 去搜尋,
不過速度上會不夠,我們需要優化一下
個人範例程式碼 - DFS + Memoization
class Solution:
def hasValidPath(self, grid: List[List[str]]) -> bool:
self.memo = {}
return self.dfs(grid, 0, 0, 0)
def dfs(self, grid, i, j, cnt):
# end of recursion
if i <mark> len(grid)-1 and j </mark> len(grid[0])-1 and grid[i][j] == ")":
return cnt == 1
if not self.is_valid(grid, i, j):
return False
if cnt < 0:
return False
# define
if grid[i][j] == "(":
cnt += 1
else:
cnt -= 1
# split
if (i, j, cnt) in self.memo:
return self.memo[(i, j, cnt)]
ans = self.dfs(grid, i+1, j, cnt) or self.dfs(grid, i, j+1, cnt)
self.memo[(i, j, cnt)] = ans
return ans
def is_valid(self, grid, i, j):
m, n = len(grid), len(grid[0])
return 0 <= i < m and 0 <= j < n
最近在練習程式碼本身就可以自解釋的 Coding style,可以嘗試直接閱讀程式碼理解
算法說明
這個是在閱讀別人的解答後,自己重寫的解法,用 cnt 優化了 “()” 的 queue 判斷式,這個想法非常的漂亮。
另外這邊我也才注意到原題目要求的搜索方向固定只有「右」和「下」,
因此多方向的寫法其實也可以簡化得更漂亮。
判定條件
結束條件:
- 「i = len(grid)-1」 and 「j = len(grid[0])-1」判定結束位置在右下角
- grid[i][j] = “)",結束必須為 “)”
- return cnt = 1 (我們也必須要知道的是,剩下個括弧數剛好等於 1,等於只剩「”("」)
終止條件:
- 當 cnt < 0 ,表示只有 “)",retrun False
- 當不在範圍內時,return False
Memoization 筆記 (記憶化搜索)
Memoization 記憶化搜索是解決這個 TLE 的關鍵,
簡單來說就是我們把「重複性」且「已經解過的問題」,做解答的筆記。
- 如果說,DFS 是從起點往終點搜尋
- Memoization,就是類似從終點往回看的過程紀錄 (類似 DP 概念)
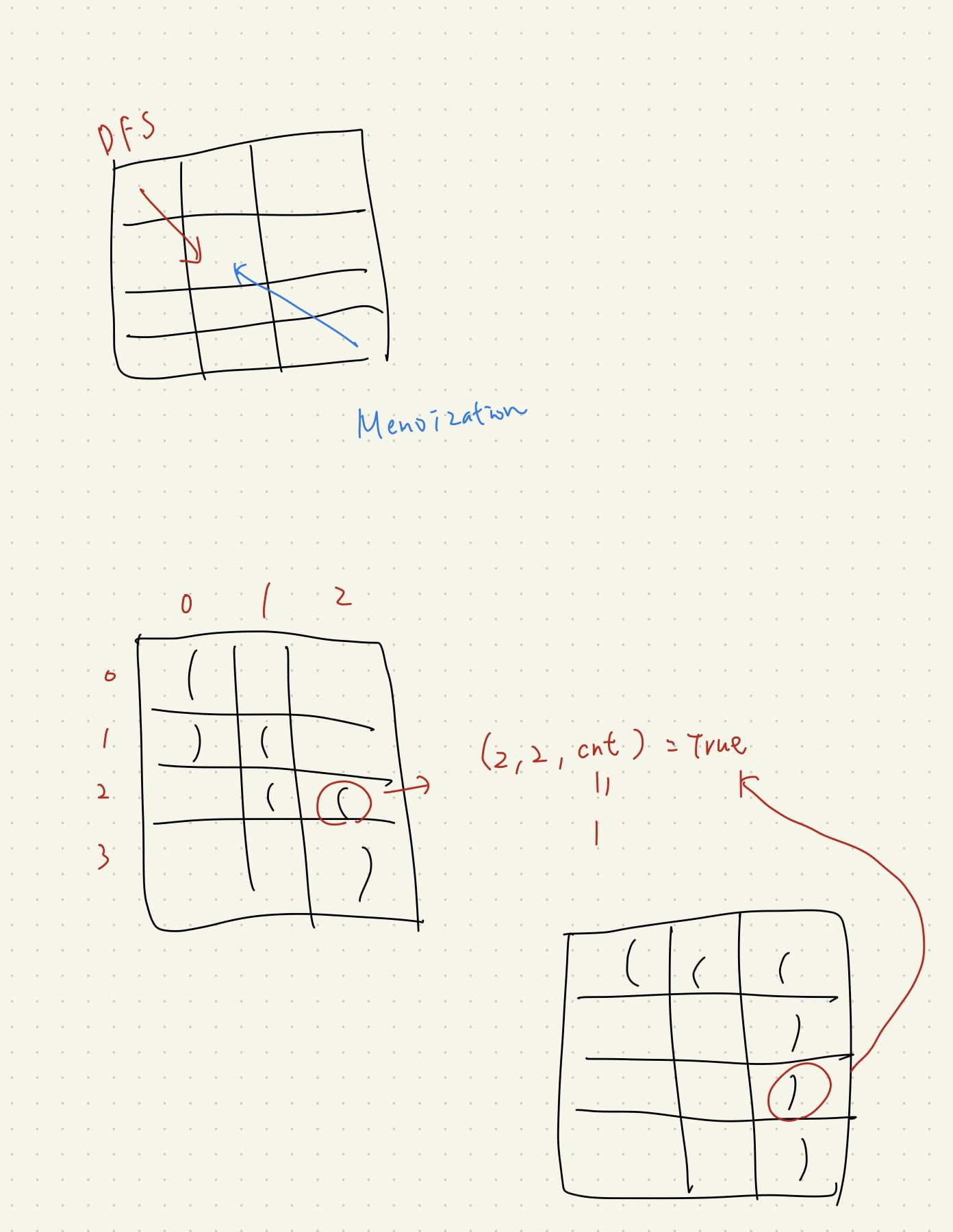
以下面的圖片來說明,可能路線可能有非常多種,
但我們可以知道只要到「特定座標」,且「特定 cnt」,
就是一個重複性的題目,我們可以先把結果記錄下來。
下面看圖應該會更明顯,我們用兩種不同的路線都抵達了 (2, 2),
而我們只需要計算第一次,之後就直接從 memo 找結果,不用再計算了。
你可能會想問,這樣我們怎麼省時間的?
上面我們是用 True 為舉例比較好懂,
但他更可以替我們省下大量的 False 的時間,
因為我們也能夠以同樣概念的做 (2, 2, 0) = False (我隨便舉例的,理論上不可能)
這樣我們第二次碰到 (2, 2, 0) 這題目時 (從不同路線抵達此處,也呈現同樣狀態),
就可以不用再往下重搜了,直接回傳 False。
input handling
同 dfs 結束條件,一起在 dfs 內部處理
Boundary conditions
當上述終止條件或結束條件觸發時,return。