題目出處
難度
medium
個人範例程式碼 - DFS (會 TLE)
class Solution:
def countSubstrings(self, s: str) -> int:
ans = 0
return self.dfs(s, 0)
def dfs(self, s, start):
# end of recursion
if start >= len(s):
return 0
ans = 0
# define
for end in range(start, len(s)):
if self.is_palindromic(s[start:end+1]):
ans += 1
# split
return ans + self.dfs(s, start+1)
def is_palindromic(self, s):
# print(s)
start = 0
end = len(s)-1
while start <= end:
if s[start] == s[end]:
start += 1
end -= 1
else:
return False
return True
算法說明
DFS 的作法,應該會是最直覺地把所有可能性都舉出來,
總共會花大約 O(2^n) 的時間,會造成 TLE
input handling
一同在 DFS 內處理
Boundary conditions
在 DFS 內處理,發現 start >= end 時 return
個人範例程式碼 - DP
class Solution:
def countSubstrings(self, s: str) -> int:
ans = 0
length = len(s)
dp = [[0 for start in range(length)] for end in range(length)]
for start in range(length):
for end in range(start, length):
# print(start, end)
if dp[start][end]: # already recorded
ans += 1
continue
if self.is_palindromic(s[start:end+1]):
ans += 1
tmp_start, tmp_end = start, end
while tmp_start <= tmp_end:
dp[tmp_start][tmp_end] = 1
tmp_start += 1
tmp_end -= 1
return ans
def is_palindromic(self, s):
# print(s)
start = 0
end = len(s)-1
while start <= end:
if s[start] == s[end]:
start += 1
end -= 1
else:
return False
return True
算法說明
在上方,我們知道 DFS 因為需要 O(2^n) 的運算時間會造成 TLE 後,
我們只好採取更快的策略,最直覺的我們會想到 DP
因為 DP 最擅長幫我們把解題時間從 O(2^n) 優化至 O(n^2) 的時間。
而要讓題目優化至 O(n^2) 時間,
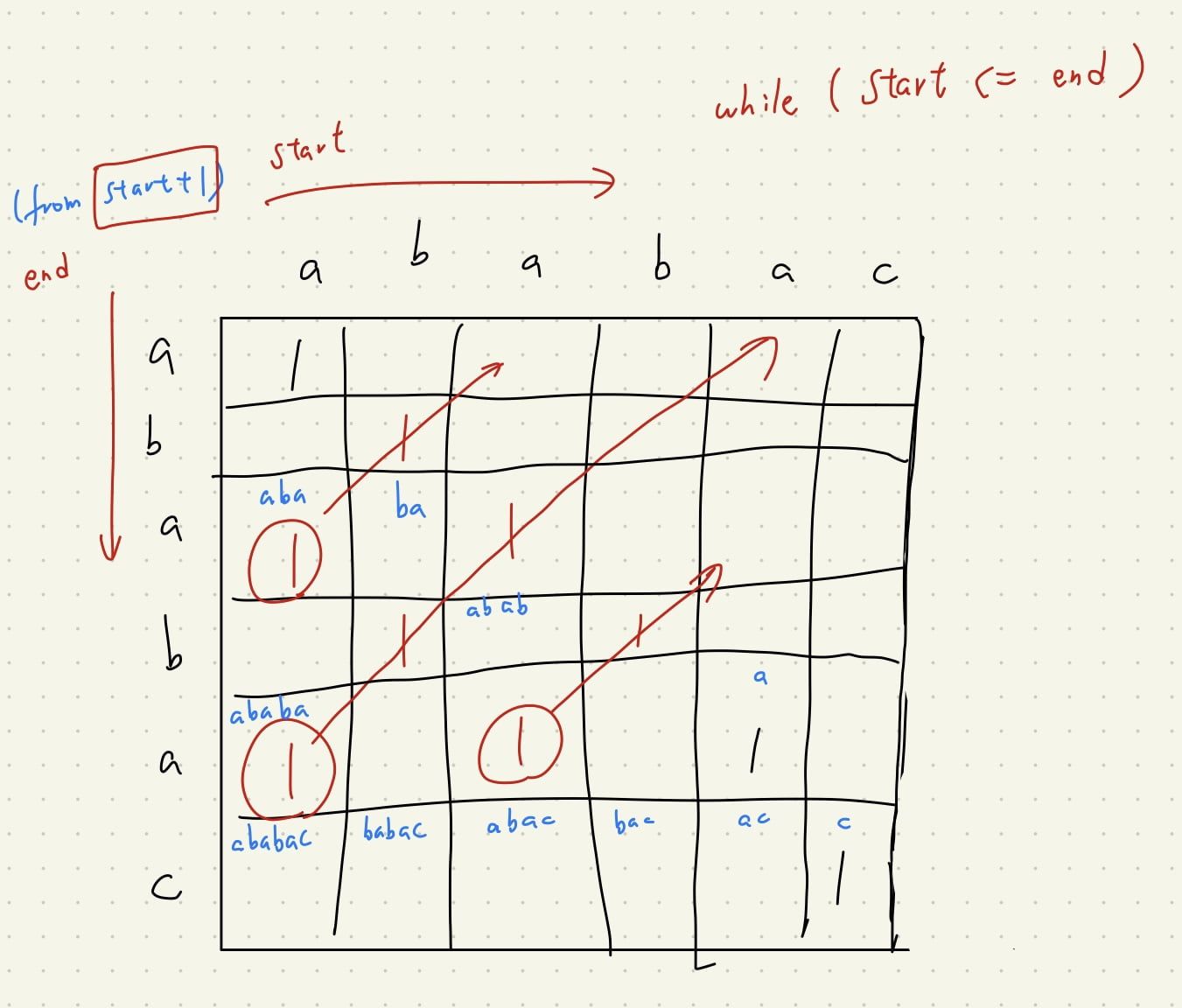
我們就先建立一個 start, end 的二維查詢表。
我們更新的方式也很簡單,
如果當發現 dp[i][j] 是 palindrome,那也表示 dp[i+1][j-1] 也是 palindrome,直到 start > end,
因此我們可以劃出上圖的紅色斜線,
判斷時,我們初始化都是 0,如果之後發現已經被改成 1,
即可 continue 直接 pass 計算。
input handling
一同在 DP 內處理
Boundary conditions
兩層 DP 的 for 迴圈,
分別代表著 start, end