前言
QuickSort 算是面試中或是演算法中經典的問題,非常重要,
而且最容易搞錯「他的範圍」,因此這邊來將自己的常見錯誤做一個總整理。
先一個正式版本
基本上,要講出 QuickSort 的核心精神,人人幾乎都不太會犯錯,
但程式非常容易寫錯,特別是在區間的控制過程。
QuickSort 的核心精神
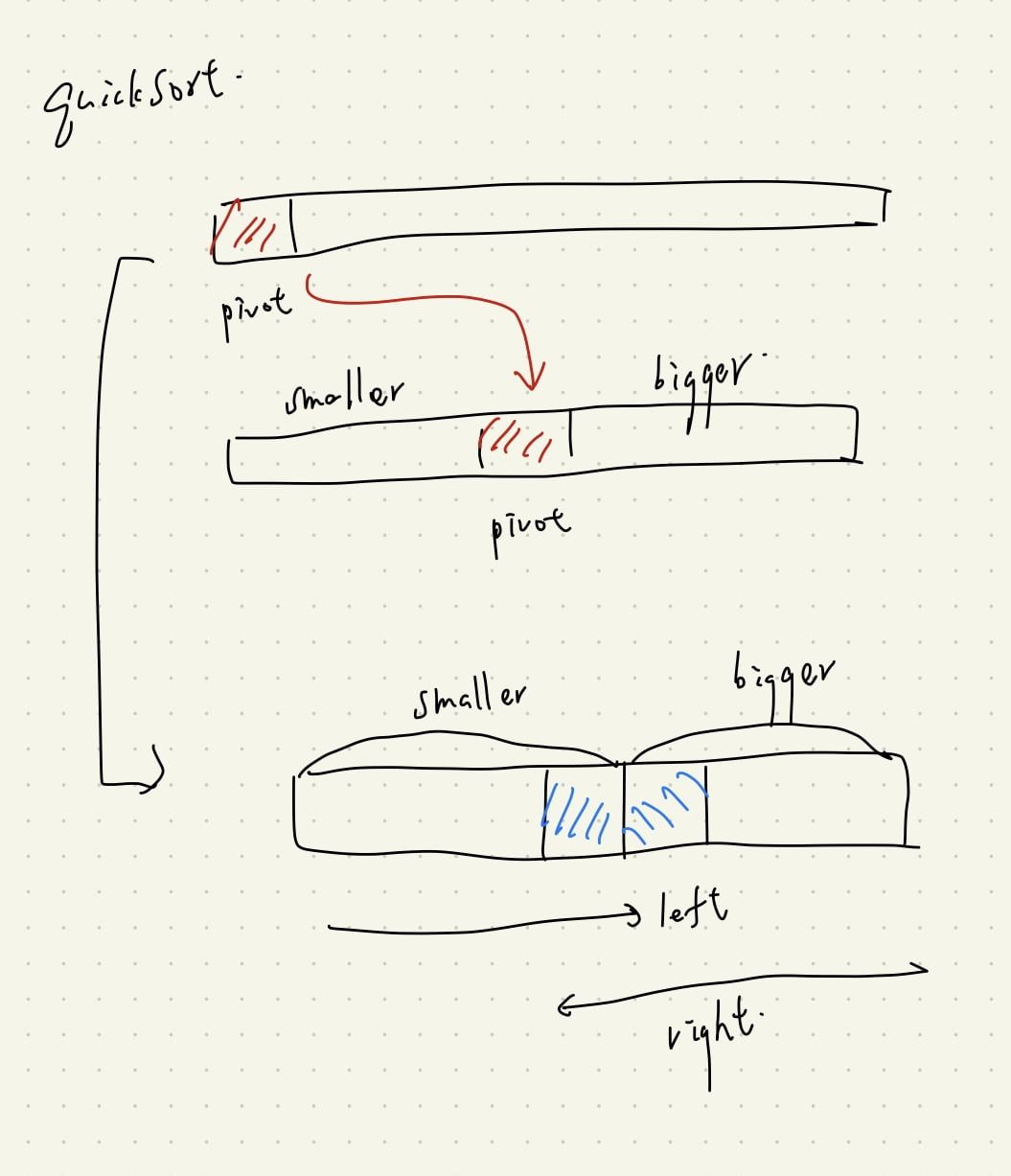
QuickSort 的核心精神就是選定一個 pivot (可以頭可以尾),
將剩下的數字透過 pivot 分成 「 < pivot 」 與 「 > pivot 」 兩組。
最容易出錯的地方 - 決定邊界
在撰寫程式的時候,如果沒有仔細思考,或甚至已經仔細思考了都還經常會寫錯。
注意:這邊示範的並「不是」主流的教科書寫法,而是用釐清觀念候「用自己的方式」寫的。
我們的目的如上圖,就是希望在循環結束時,能夠
- 讓 left 左邊的一切都是 smaller (than pivot)
- 讓 right 右邊的一切都是 bigger (than pivot)
因此 (以下為說明用的程式碼,並不完整)
while(left <= right):
while(left <= right and a[left] < pivot):
left += 1
while(left <= right and a[right] > pivot):
right -= 1
if left <= right:
a[left], a[right] = a[right], a[left]
注意啦! 光上面這裡有很多細節了!
left <= right
首先是 left <= right,如果寫 left < right 達不到交錯的效果,有可能出迴圈要多做處理
不是不能這樣寫,就是要多做一些處理,沒有什麼不能的寫法
a[left] < pivot, a[right] > pivot
注意這裡不處理等於,原因是處理等於也不一定好,
等於表示與 pivot 相等,用於處理重複的 array,
但如果硬要處理等於的情況,在 [1,1,1,1,1] 類似這樣的 case,
一定會用 worst case 的 O(n) 時間去解,而不是平均的 O(nlogN)。
可以先理解 QuickSort 的 worst case 是什麼情況及為什麼會發生,
這樣更能夠懂為什麼會舉到上面的例子。
此種類的完整的 QuickSort 程式碼
def partition(self, nums, start, end):
# recusion end
if start >= end:
return
# recursion define
left, right = start+1, end
pivot = nums[start]
while(left <= right):
while(left <= right and nums[left] < pivot):
left += 1
while(left <= right and nums[right] > pivot):
right -= 1
if left <= right:
nums[left], nums[right] = nums[right], nums[left]
else:
nums[start], nums[right] = nums[right], nums[start]
print(nums, left, right)
# recursion split
self.partition(nums, start, right-1)
self.partition(nums, left, end)
抓 partition 與 pivot 的重點
我們設計的思想是
(start) < start+1 < right < left < end
務必注意交錯的位置的「 right < left 」,這是最最重要的部分。
- 結束時,交換後 (注意交錯):
start < right-1 < pivot(right) < left < end
而 start ~ right-1 都比 pivot 小
left < end 都比 pivot 大。
結束迴圈 recursion 「start >= end」
不論是
- self.partition(nums, start, right-1)
- self.partition(nums, left, end)
right 會越來越逼近 start,直到重疊 start >= end
而 left 也會越來越逼近 end (因為 left 與 right 是交錯,只會更逼近 end)
另外一種寫法
建議先嘗試閱讀以下程式碼,思考一下
(這我寫過的東西,我也想了很久為什麼)
while(left <= right)
if a[left] < pivot:
left += 1
elif a[right] > pivot:
right -= 1
else:
a[left], a[right] = a[right], a[left]
# left += 1
# right -= 1
建議想好後再看,這樣才會更印象深刻。
注意 left <= right
一樣要注意的 left <= right,因為一定要交錯。
「left += 1」、「right -= 1」可有可無
其中「left += 1」、「right -= 1」可有可無,
沒有當下處理也會在之後的迴圈被處理掉。
此種類的完整的 QuickSort 程式碼
def partition(self, nums, start, end):
# recusion end
if start >= end:
return
# recursion define
left, right = start+1, end
pivot = nums[start]
while(left <= right):
if nums[left] < pivot:
left += 1
elif nums[right] > pivot:
right -= 1
else:
nums[left], nums[right] = nums[right], nums[left]
else:
nums[start], nums[right] = nums[right], nums[start]
# recursion split
self.partition(nums, start, right-1)
self.partition(nums, left, end)
抓 partition 與 pivot 的重點
我們設計的思想是
(start) < start+1 < right < left < end
務必注意交錯的位置的「 right < left 」,這是最最重要的部分。
- 結束時,交換後 (注意交錯):
start < right-1 < pivot(right) < left < end
而 start ~ right-1 都比 pivot 小
left < end 都比 pivot 大。
結束迴圈 recursion 「start >= end」
不論是
- self.partition(nums, start, right-1)
- self.partition(nums, left, end)
right 會越來越逼近 start,直到重疊 start >= end
而 left 也會越來越逼近 end (因為 left 與 right 是交錯,只會更逼近 end)